Question

hello, there can help me with this question.A grove of redwood tree has an estimated 3,400,000 board feet of lumber at thestart of 2022. If redwoods grow at an exponential rate of 9% each year, then whatwould be the growth formula? Within which year will the grove reach one billion boardfeet of lumber?

Answer 1

Step-by-step explanation:

a) Firstly, we want to write the growth formula

We have the general form as:

`L\text{ = I\lparen1 + r\rparen}^t`

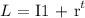
where:

L is the estimated board feet of lumber

l is the is the initial estimated board feet of lumber (the initial estimated board feet of lumber in 2022)

r is the percentage rate of increase which is 9% (9/100 = 0.09)

t is the number of years to reach the estimated board feet of lumber

With respect to the question given, we have the formula as:

`\begin{gathered} L\text{ = 3,400,00\lparen1 + 0.09\rparen}^t \\ L\text{ =3,400,000\lparen1.09\rparen}^t \end{gathered}`

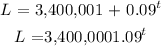
b) We want to get the value of t when L is 1 billion

Substituting the values, we have it that:

`\begin{gathered} 1000000000\text{ = 3400000\lparen1.09\rparen}^t \\ divide\text{ both sides by 3,400,000} \\ 294.12\text{ = 1.09}^t \\ ln\text{ 294.12 = tln 1.09t } \\ t\text{ = }\frac{ln\text{ 249.12}}{ln\text{ 1.09}}\text{ = 66 years} \end{gathered}`

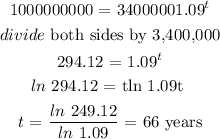
In 66 years (2088) , the groove will reach one billion board feet of lumber