Answer:
- 3log(10) -2log(5) ≈ 1.60206
- no; rules of logs apply to any base. ln(x) ≈ 2.302585×log(x)
- no; the given "property" is nonsense
Explanation:
1.
The given expression expression can be simplified to ...
3log(10) -2log(5) = log(10^3) -log(5^2) = log(1000) -log(25)
= log(1000/25) = log(40) . . . . ≠ log(5)
≈ 1.60206
Or, it can be evaluated directly:
= 3(1) -2(0.69897) = 3 -1.39794
= 1.60206
__
2.
The properties of logarithms apply to logarithms of any base. Natural logs and common logs are related by the change of base formula ...
ln(x) = log(x)/log(e) ≈ 2.302585·log(x)
__
3.
The given "property" is nonsense. There is no simplification for the product of logs of the same base. There is no expansion for the log of a sum. The formula for the log of a power does apply:
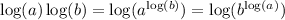
Numerical evaluation of Mr. Kim's expression would prove him wrong.
log(3)log(4) = (0.47712)(0.60206) = 0.28726
log(7) = 0.84510
0.28726 ≠ 0.84510
log(3)log(4) ≠ log(7)