Question

Please help me with this question so my son can better understand. What is the product of (-2x^3 + x - 5 ) and (x^3 - 3x - 4 )?(a)Show your work.(b)Is the product of (-2x^3 + x - 5 ) and (x^3 - 3x - 4 ) equal to the product of (x^3- 3x - 4) and (-2x^3 + x - 5 )? Explain your answer.

Answer 1

a)

`-2x^6+7x^4+3x^3-3x^2+11x+20`

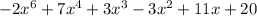
b) The product of (-2x^3 + x - 5 ) and (x^3 - 3x - 4 ) is equal to the product of (x^3 - 3x - 4) and (-2x^3 + x - 5 ) since, according to the commutative property of multiplication, changing the order of the numbers being multiplied does not change the product.

Step-by-step explanation:

Given the expressions;

`\begin{gathered} \mleft(-2x^3+x-5\mright) \\ \text{and } \\ (x^3-3x-4) \end{gathered}`

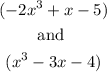
a) To determine the product of the above expressions, we have to use each term in the first expression to multiply each term in the second expression as seen below below;

`\begin{gathered} (-2x^3+x-5)*\mleft(x^3-3x-4\mright) \\ =(-2x^3\cdot x^3)+\lbrack-2x^3(-3x)\rbrack+\lbrack-2x^3(-4)\rbrack+(x\cdot x^3)+\lbrack x(-3x)\rbrack \\ +\lbrack x(-4)\rbrack+(-5\cdot x^3)+\lbrack-5(-3x)\rbrack+\lbrack-5(-4)\rbrack \end{gathered}`
`\begin{gathered} =-2x^6+6x^4+8x^3+x^4-3x^2-4x-5x^3+15x+20 \\ =-2x^6+7x^4+3x^3-3x^2+11x+20 \end{gathered}`

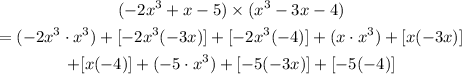
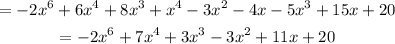
So the product of (-2x^3 + x - 5 ) and (x^3 - 3x - 4 ) is;

`-2x^6+7x^4+3x^3-3x^2+11x+20`

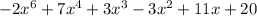
b) Note that the commutative property of multiplication states that changing the order of the numbers being multiplied does not change the product.

So we can say that the product of (-2x^3 + x - 5 ) and (x^3 - 3x - 4 ) is equal to the product of (x^3 - 3x - 4) and (-2x^3 + x - 5 ) since, according to the commutative property of multiplication, changing the order of the numbers being multiplied does not change the product.