Height of the ball:
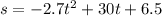
a) Find t for a height (s) of 20ft:
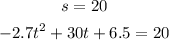
Solve t:
1. Subtract 20 in both sides of the equation:
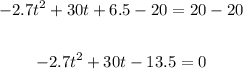
2. Use quadratic formula to solve t:
![\begin{gathered} ax^2+bx+c=0 \\ \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/7aff8mm3mfsnzv3fikx7rosnjx11m76p6i.png)
![\begin{gathered} t=\frac{-30\pm\sqrt[]{30^2-4(-2.7)(-13.5)}}{2(-2.7)} \\ \\ t=\frac{-30\pm\sqrt[]{900-145.8}}{-5.4} \\ \\ t=\frac{-30\pm\sqrt[]{754.2}}{-5.4} \\ \\ t_1=\frac{-30+\sqrt[]{754.2}}{-5.4}=0.47 \\ \\ t_2=\frac{-30-\sqrt[]{754.2}}{-5.4}=10.64 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/gudzbcb1zf4coilcawdmitvb9vie1iva3s.png)
Then, the height of the ball is 20ft above the moon's surface after 0.47seconds and 10.64seconds
b) The ball will hit the moon's surface when its height is 0ft.
Use the given function for the height of the ball and solve t when s=0:
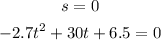
Find t using quadratic formula:
![\begin{gathered} t=\frac{-30\pm\sqrt[]{30^2-4(-2.7)(6.5)}}{2(-2.7)} \\ \\ t=\frac{-30\pm\sqrt[]{900-70.2}}{-5.4} \\ \\ t=\frac{-30\pm\sqrt[]{829.8}}{-5.4} \\ \\ t_1=\frac{-30+\sqrt[]{829.8}}{-5.4}=0.22 \\ \\ t_2=\frac{-30-\sqrt[]{829.8}}{-5.4}=10.89 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/niy0zf568uiwa844x2q4ozmu7afgfsum65.png)
Then, the ball hit the moon's surface at 0.22 seconds and 10.89 seconds