Question

Select the correct answer.Given the focus and directrix shown on the graph, what is the vertex form of the equation of the parabola?

Answer 1

Answer: X =
`(1)/(10)` ( y - 3
`)^(2)` -
`(3)/(2)`

Step-by-step explanation: Correct on Edmentum

Answer 2

The directrix of the parabola is a vertical line at x = -4 and the focus is at the right of the directrix at (1, 3). This means the parabola is horizontal and it opens to the right.

The equation of a vertical parabola is:

`x=(1)/(4p)(y-k)^2+h`

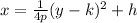
Where (h, k) are the vertex coordinates, and the vertex is at the midpoint between the focus and the directrix.

The y-coordinate of the vertex is k = 3 and the x-coordinate is:

`h=(-4+1)/(2)=-(3)/(2)`

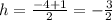
p is the distance from the vertex to the focus:

`p=-(3)/(2)+4=(5)/(2)`

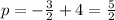
Thus:

`4p=4\cdot(5)/(2)=10`

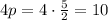
Now we can substitute all the values into the equation:

`x=(1)/(10)(y-3)^2-(3)/(2)`

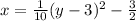
This is the required vertex form of the parabola.