Given:
The point M is midpoint of line segment AC.
And co-ordinates are A(0,0) and C(c,d).
Find the co-ordinates of midpoint M,
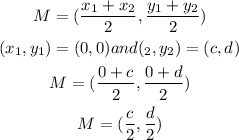
Similarly, the co-ordinates of point N whch is midpoint of line CB,
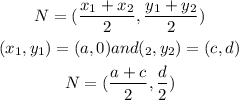
Now find the slope of line MN,
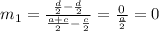
Slope of line AB is,
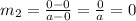
The two lines are parallel if their slopes are equal.
From the above steps line MN and Line AB have the equal slope.
It implies that both the line MN and AB are parallel.
Hence, it is proved that the segment joining the midpoints of two sides of a triangle is parallel to the third side.