Question

Find the points of inflection and discuss the concavity of the graph of the function.

Answer 1

The points of inflection of a function are given by the zeros of the second derivative. The first derivative of our function is:

`f^(\prime)(x)=2(-\csc(3x)/(2)\cot(3x)/(2))\cdot(3)/(2)=-3(\csc(3x)/(2)\cot(3x)/(2))`

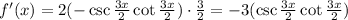
Using the product rule, the second derivative of our function is:

`\begin{gathered} f^(\prime)^(\prime)(x)=-3\lbrack(\csc(3x)/(2))^(\prime)\cdot(\cot(3x)/(2))+(\csc(3x)/(2))\cdot(\cot(3x)/(2))^(\prime)\rbrack \\ \\ =(9)/(2)(\csc(3x)/(2)\cot^2(3x)/(2)+\csc^3(3x)/(2)) \end{gathered}`

Then, the zeros of the second derivative are the solutions for the following equation:

`(9)/(2)(\csc(3x)/(2)\ctg^2(3x)/(2)+\csc^3(3x)/(2))=0`

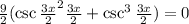
Simplifying this expression, we have:

`\begin{gathered} (9)/(2)(\csc(3x)/(2)\ctg^2(3x)/(2)+\csc^3(3x)/(2))=0 \\ \\ \csc(3x)/(2)\ctg^2(3x)/(2)+\csc^3(3x)/(2)=0 \\ \\ \ctg^2((3x)/(2))+\csc^2((3x)/(2))=0 \\ \\ \cos^2((3x)/(2))+1=0 \\ \\ \cos^2((3x)/(2))=-1\implies\\exists x\in\mathbb{R} \end{gathered}`

Our function has no inflection points.