Given the following expression:
![2x\sqrt[]{44x}-2\sqrt[]{11x^3^{}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/y53howcsxp1sggegkgm1zfkae4vxndt70i.png)
You can follow the steps shown below in order to find an equivalent expression. But first, it is important to remember that an equivalent expression can be found by simpliying an expression.
1. According to the Product of Powers property:
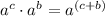
Then, you can rewrite the expression as following:
![2x\sqrt[]{44x}-2\sqrt[]{11x\cdot x^2}](https://img.qammunity.org/2023/formulas/mathematics/high-school/answsy1nnryqc6oimmtu4kmwjdrv51w7ix.png)
2. Descompose 44 into its prime factors:
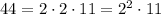
3. Substitute the above into the expression:
![=2x\sqrt[]{2^2\cdot11x}-2\sqrt[]{11x\cdot x^2}](https://img.qammunity.org/2023/formulas/mathematics/high-school/9t8ksk3ocvu3xgatq72x9uy98ehfbymsdm.png)
4. Remember the following property for Radicals:
![\sqrt[n]{a^n}=a](https://img.qammunity.org/2023/formulas/mathematics/college/iip6mtffd1c87x2h11rrrir6hfqw2jfavg.png)
5. Then, you can simplify the expression:
![\begin{gathered} =(2x)(2)\sqrt[]{11x}-(2)(x)\sqrt[]{11x^{}} \\ =4x\sqrt[]{11x}-2x^{}\sqrt[]{11x} \\ =2x\sqrt[]{11x} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/7lmj4d3cght2jzgtd52odzziixdbo0131g.png)
The answer is: Option A.