Question

Find the sum of the first 20 terms of the arithmetic series 53,46,39,32...

Answer 1

The answer can be found by assuming that we have an arithmetic progression that stars in 53 with a common difference of 7. The equation for the sum of an arithmetic progression up to n terms is given by:

`s_n=(n)/(2)(2a+(n-1)d)`

Where, for this case

`a=53\text{ , }n=20\text{ and }d=7`

So, applying the equation with these data, we obtain:

`\begin{gathered} s_(20)=(20)/(2)(2(53)+(20-1)7) \\ s_(20)=10(106+19(7)) \\ s_(20)=10(106+19(7))=10(239)=2390 \end{gathered}`

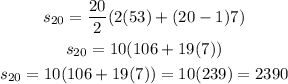
Thus, the sum up to 20 terms of the given series is 2390.