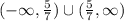Question

What would the inverse be of the function f? What would the inverse domain and range be?

Answer 1

Given the function

`f(x)=(4x+4)/(7x-5)`

The inverse is given by

Replace f(x) with y:

`y=(4x+4)/(7x-5)`

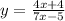
Swap x with y:

`x=(4y+4)/(7y-5)`

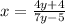
Solve for y:

`\begin{gathered} x(7y-5)=(4y+4)/(7y-5)(7y-5) \\ x(7y-5)=4y+4 \\ 7xy-5x=4y+4 \\ 7xy-5x+5x=4y+4+5x \\ 7xy=4y+4+5x \\ 7xy-4y=4y+4+5x-4y \\ 7xy-4y=4+5x \end{gathered}`

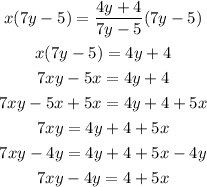
Factor

`\begin{gathered} y(7x-4)=4+5x \\ y((7x-4))/((7x-4))=(4+5x)/(7x-4) \\ y=(4+5x)/(7x-4) \end{gathered}`

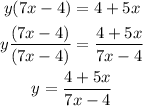
Answer:

the inverse of function f is, replace y with f^-1(x)

`f^(-1)(x)=(4+5x)/(7x-4)`

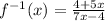
Domain of f^-1

These are the x-values of the function. First, Find undefined points

`\begin{gathered} 7x-4\\e0 \\ 7x-4+4\\e0+4 \\ 7x\\e4 \\ (7x)/(7)\\e(4)/(7) \\ x\\e(4)/(7) \end{gathered}`

We have that x must be different from 4/7 therefore the domain is:

`\begin{gathered} x<(4)/(7) \\ or\text{ } \\ x>(4)/(7) \end{gathered}`

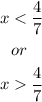
Answer:

in interval notation

`(-\infty,(4)/(7))\cup((4)/(7),\infty)`

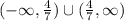
Range of f^-1

These are the values and for which the function is defined. In this case, we have that given a function f and its inverse the domain of f becomes the range of f^-1. Therefore, we find the domain of the function f:

`\begin{gathered} Restrictions \\ 7x-5\\e0 \\ 7x-5+5\\e0+5 \\ 7x\\e5 \\ (7x)/(7)\\e(5)/(7) \\ x\\e(5)/(7) \end{gathered}`

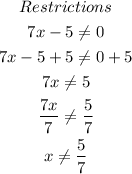
We have that x must be different from 5/7, so:

`\begin{gathered} x<(5)/(7) \\ or \\ x>(5)/(7) \end{gathered}`

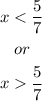
Combining the ranges

`\begin{gathered} f(x)<(5)/(7) \\ or \\ f(x)>(5)/(7) \end{gathered}`

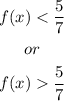
Answer:

the range in interval notation

`(-\infty,(5)/(7))\cup((5)/(7),\infty)`