Question

Suppose that shoe sizes of American women have a bell-shaped distribution with a mean of 8.15 and a standard deviation of 1.48. Using the empirical rule, what percentage of American women have shoe sizes that are greater than 11.11? Please do not round your answer.

Answer 1

To find the percentage of American women who have shoe sizes that are greater than 11.11, we apply the z score formula first

The z score formula is

`\begin{gathered} z=(x-\mu)/(\sigma) \\ Where\text{ } \\ The\text{ observed value, x}=11.11 \\ The\text{ mean, }\mu=8.15 \\ The\text{ standard deviation, }\sigma=1.48 \end{gathered}`

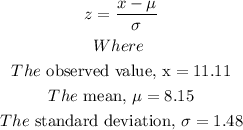
Substitute the variables into the formula above

`\begin{gathered} z=(11.11-8.15)/(1.48)=(2.96)/(1.48)=2 \\ z=2 \end{gathered}`

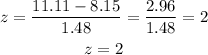
Given that the z = 2

From the deduction above, the given value is 2 standard deviation away to the right of the mean.

According to the empirical rule,

Using the chart below

The percentage of American women who have shoe sizes that are greater than 11.11 is

`=2.35+0.15=2.5\%`

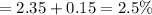
Hence, the answer is 2.5%