Question

An airplane flies 3300 miles into the wind for 15 hours. The return trip takes 11 hours. Find the speed of the airplane without a wind and the speed of the wind.The speed of the airplane without the wind is ___ miles/hrThe speed of the wind is ___ miles/hour.

Answer 1

Speed, s, is defined as the distance, d, divided by time, t, that is,

`s=(d)/(t)`

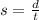
Defining the next variables:

a: speed of the airplane, in mph

w: speed of wind, in mph

In the first case, the combined speed is obtained subtracting the speed of wind to the speed of the airplane. The distance traveled is 3300 miles, and time elapsed is 15 hours. Substituting in the formula:

`\begin{gathered} a-w=(3300)/(15) \\ a-w=220 \end{gathered}`

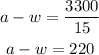
In the second case, the combined speed is obtained adding both individual speeds. The distance traveled is 3300 miles, and time elapsed is 11 hours. Substituting in the formula:

`\begin{gathered} a+w=(3300)/(11) \\ a+w=300 \end{gathered}`

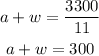
Adding these two equations:

`\begin{gathered} (a-w)+(a+w)=(3300)/(15)+(3300)/(11) \\ a+a-w+w=300+220 \\ 2a=520 \\ a=(520)/(2) \\ a=260\text{ mph} \end{gathered}`

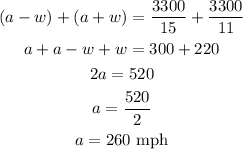
Replacing this result in the second equation and solving for w:

`\begin{gathered} 260+w=300 \\ w=300-260 \\ w=40\text{ mph} \end{gathered}`

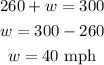
The speed of the airplane without the wind is 260 miles/hr



The speed of the wind is 40 miles/hour.