Question

Solve the problem. The daily profit in dollars made by an automobile manufacturer is P(x) = -45r2 +2,430x - 15,000 where x is the number of cars produced per shift . How many cars must be produced per shift for the company to maximize its profit?

Answer 1

Let's find the first derivative of the function:

`\begin{gathered} P(x)^(\prime)=2(-45)x+2430^{} \\ P(x)^(\prime)=-90x+2430 \end{gathered}`

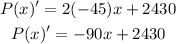
Let's find the critical point, in order to find its maximum:

`\begin{gathered} P(x)^(\prime)=0 \\ -90x+2430=0 \\ \text{solve for x:} \\ 90x=2430 \\ x=(2430)/(90) \\ x=27 \end{gathered}`

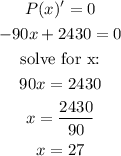
xo is a global maximum for the function if:

`f\colon X\to R,if_{\text{ }}(x\in R)f(x_o)\ge x`

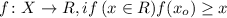
So:

`\begin{gathered} x<27 \\ x=26 \\ P(26)=17760 \\ x>27 \\ x=28 \\ P(28)=17760 \\ x=27 \\ P(27)=17805 \\ so\colon \\ P(27)>P(28)>P(26) \end{gathered}`

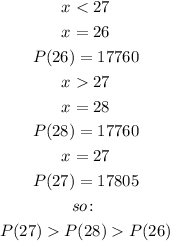
Therefore, x is the global maximum of the function, therefore, the automobile manufacturer needs to produce 27 cars per shift in order to maximize its profit