Question

Determine whether the given ordered pair is a solution to the system of equations.5x−y =4 x+6y =2 Ordered pair: (4,0)

Answer 1

Given the system of equations:

`\begin{gathered} 5x-y=-4\text{ -- equation 1} \\ x+6y=2\text{ --- equation 2} \end{gathered}`

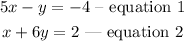
To determine if the ordered pair (4, 0) is a solution to the system of equations, we solve for x and y.

Thus, by the substitution method of solving simultaneous equations, we have

from equation 1,

`\begin{gathered} make\text{ y the subject of formula,} \\ y=5x+4---\text{ equation 3} \end{gathered}`

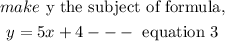
Substitute equation 3 into equation 2.

Thus, we have

To solve for y, substitute the obtained value of x into equation 3.

Thus,

`y=5(-(22)/(31))+4=(14)/(31)`

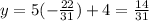
Thus, the solution to the system of equations is

`(x,y)\Rightarrow(-(22)/(31),(14)/(31))`

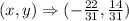
Hence, the ordered pair (4, 0) is NOT a solution to the system of equations.