Question

How can I solve 10x-3y-81=0 and-5x-7y-19=0 with Elimination?

Answer 1

To solve the given system of equation as it was given by the elimination method, the first step is to multiply the whole second equation by 2. If we multiply both, the left and right sides by 2, the equality will be maintained, as follows:

`\begin{gathered} 10x-3y-81=0 \\ 2*(-5x-7y-19=0)\to-10x-14y-38=0 \end{gathered}`

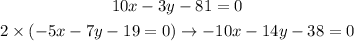
Now, we can sum both equations, as follows:

`\begin{gathered} (10x-3y-81)+(-10x-14y-38)=0+0 \\ -17y-119=0\to17y+119=0 \end{gathered}`

By isolating y, we can find its value as follows:

`\begin{gathered} 17y=-119\to y=-(119)/(17) \\ y=-7 \end{gathered}`

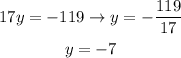
Now, we find the value of x by substituting the y in the first equation, as follows:

`\begin{gathered} 10x-3*(-7)-81=0\to10x+21-81=0 \\ 10x=60\to x=(60)/(10) \\ x=6 \end{gathered}`

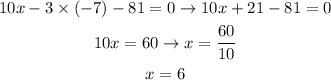
From the solution developed above, we are able to conclude the values of x and y:

x = 6 ; y = - 7