Question

find the equation of the linr tangent to the function ay the given point. Answer has to be in slope intercept form

Answer 1

`y=(1)/(2)x+3`

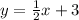
Step-by-step explanation

Sep 1

Find the first derivative of f(x)

`\begin{gathered} y=(5x+5)^{(1)/(2)} \\ \text{derivate applyin the chain rule} \\ y^(\prime)\text{ = }(1)/(2)(5x+5)^{(1)/(2)-(2)/(2)}\cdot(5) \\ y^(\prime)\text{ = }(1)/(2)(5x+5)^{-(1)/(2)}\cdot(5) \\ y^(\prime)\text{ = }(5)/(2)(5x+5)^{-(1)/(2)} \\ \text{ y'= }(5)/(2)(5x+5)^{-(1)/(2)} \end{gathered}`

Step 2

Plug x value of the indicated point into f '(x) to find the slope at x.

so

Therefore, at x = 4, the slope of the tangent line is

`\begin{gathered} \text{ y'= }(5)/(2)(5(4)+5)^{-(1)/(2)} \\ \text{ y'= }(5)/(2)(25)^{-(1)/(2)} \\ \text{ y'= }(5)/(2)\cdot\frac{1}{\sqrt[]{25}} \\ \text{ y'= }(5)/(2)\cdot(1)/(5)=(1)/(2) \\ so,\text{ the slope is 1/2} \end{gathered}`

Step 3

finally, find the equation of the lne by using

`\begin{gathered} y-y_1=m(x-x_1) \\ \text{where m is the slope} \\ \text{and ( x}_1,y_1)\text{ is a point of the line, } \\ \text{hence, replace} \\ y-5=(1)/(2)(x-4) \\ y-5=(1)/(2)x-2 \\ \text{add 5 in both sides} \\ y-5+5=(1)/(2)x-2+5 \\ y=(1)/(2)x+3 \end{gathered}`

so, the answer is

`y=(1)/(2)x+3`

I hope this helps you