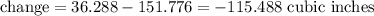Question

If the cutout length increases from 0.6 to 2.4 in what is the change in the box's volume

Answer 1

If the length of the cut-out was "x" inches, then the length of the box is:

`\text{length}=15-2x`

The width of the box is:

`\text{width}=11-2x`

The height is:

`\text{height}=x`

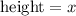
The volume of the box is given by:

`\begin{gathered} \text{volume = height}\cdot\text{ width}\cdot\text{ height} \\ \text{volume}=(15-2x)(11-2x)x \end{gathered}`

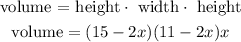
If the cutout was 0.6 inches. The volume is:

`\begin{gathered} \text{volume}(0.6)=(15-2\cdot0.6)(11-2\cdot0.6)\cdot0.6 \\ \text{volume}(0.6)=13.8\cdot9.8\cdot0.6=81.144\text{ cubic inches} \end{gathered}`

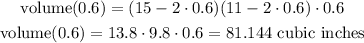
If the cutout was 2.4 inches.

`\begin{gathered} \text{volume}(2.4)=(15-2\cdot2.4)\cdot(11-2\cdot2.4)\cdot2.4 \\ \text{volume}(2.4)=10.2\cdot6.2\cdot2.4=151.776\text{ cubic inches} \end{gathered}`

The change on the volume of the box is the difference between the two volumes above:

`\text{change}=151.776-81.144=70.632\text{ cubic inches}`

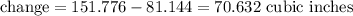
If the cutout was 4.8 inches.

`\begin{gathered} \text{volume}(4.8)=(15-2\cdot4.8)\cdot(11-2\cdot4.8)\cdot4.8 \\ \text{volume}(4.8)=5.4\cdot1.4\cdot4.8=36.288_{}\text{ cubic inches} \end{gathered}`

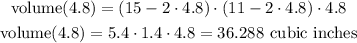
The change on the volume of the box is the difference between the volumes from when the cutout was 4.8 inches and 2.4 inches.

`\text{change}=36.288-151.776=-115.488\text{ cubic inches}`