Question

Photo is includedsolve the following system of inequalities graphically on the set of axes below

Answer 1

fromAre you the question;

we will be solving for

`\begin{gathered} 3x\text{ + y }<\text{ 7} \\ y\text{ }\ge\text{ }(2x)/(3)\text{ - 4} \end{gathered}`

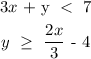
Solving the first inequality

`\begin{gathered} 3x\text{ + y }<7 \\ we\text{ have } \\ 3x\text{ + y = 7} \\ \text{when x = 0} \\ y\text{ = 7} \\ \text{when y = 0} \\ 3x\text{ = 7} \\ x\text{ = 7/3} \end{gathered}`

Therefore,

For the first inequality

`\begin{gathered} 3x\text{ + y }<7 \\ we\text{ have the points (0, 7) and (}(7)/(3),\text{ 0)} \end{gathered}`

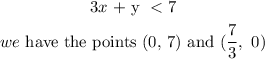
For the second inequality

`\begin{gathered} y\text{ }\ge\text{ }(2x)/(3)\text{ - 4} \\ we\text{ have } \\ y\text{ = }(2x)/(3)\text{ - 4} \\ \text{when x = 0} \\ y\text{ = - 4} \\ \text{when y = 0} \\ 0\text{ = }(2x)/(3)\text{ - 4} \\ 4\text{ = }(2x)/(3) \\ 12\text{ = 2x} \\ x\text{ = 6} \end{gathered}`

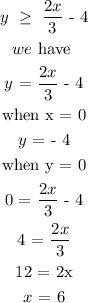
Therefore,

For the second inequality

`\begin{gathered} y\text{ }\ge\text{ }(2x)/(3)\text{ - 4} \\ we\text{ have the points (0, -4) and ( 6, 0)} \end{gathered}`

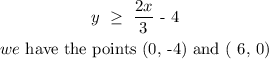
We will be plotting the graph of the inequalities using the appropriate points

The graph above shows the graph of the inequalities

The overlapping region(purple region) shows the solution of the inequalities