Question

Need step by step solution. Check the convergence of the given series.

Answer 1

Given the series

`\sum ^(\infty)_(n\mathop=1)n^2e^(-n)`

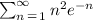
The n-th term of the series is

`a_n=n^2e^(-n)`

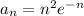
Use the ratio test to check the convergence.

`\begin{gathered} \rho=\lim _(n\to\infty)(a_(n+1))/(a_n) \\ =\lim _(n\to\infty)((n+1)^2e^(-(n+1)))/(n^2e^(-n)) \\ =\lim _(n\to\infty)(1+(1)/(n))^2e^(-1) \\ =e^(-1) \end{gathered}`

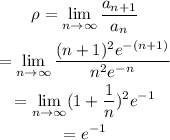
If the limit is less than 1, the series converges. If the limit is greater than 1, then the series diverges and if it equals 1, then the test fails.

Here the value of the limit is < 1, since e > 1. So, the given series converges.