The ratio of the lengths of corresponding sides of 2 similar triangles is 4 to 1. Therefore, the ratio of the areas of the two triangles is ______ to 1.

Question

asked Jan 14, 2023 81.8k views

1 Answer

BrandonAGr · Answer 1 · 2023-01-19T05:21:30+0000

Given that the ratio of the lengths of corresponding sides of 2 similar triangles is 4 to 1.

The ratio of the area of two similar triangles is proportional to the square of the ratio of their corresponding sides.

Therefore, the ratio of the areas of the two triangles is

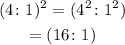
$\begin{gathered} (4\colon1)^2=(4^2\colon1^2) \\ =(16\colon1) \end{gathered}$

Hence, the ratio of the areas of the two triangles is 16 to 1