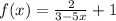Question

Yea thanks for your time to reply I love

Answer 1

Given: The derivative of the function is given as

`(df)/(dx)=(10)/((3-5x)^2)`

The antiderivative is guessed as

`f(x)=(2)/(3-5x)`

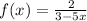
Required:

(a) Is the guess correct?

(b) Is it the only possible answer?

(c)Find another anti derivative if possible.

Step-by-step explanation:

To find the antiderivative, we must integrate the derivative

`\begin{gathered} \int(df)/(dx)=\int(10)/((3-5x)^2) \\ f(x)=(-10)/(3-5x)((-1)/(5))+c \end{gathered}`

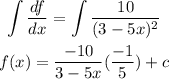
where c is a constant.

Now,

`f(x)=(2)/(3-5x)+c`

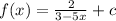
(a)

For c = 0

`f(x)=(2)/(3-5x)`

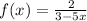
So the guess is correct.

(b)

There can be many other answers, by putting different values of c, we can get different antiderivatives.

So, student answer is not the only possible answer.

(c)

For any other anti-derivative, put c = 1

`f(x)=(2)/(3-5x)+1`

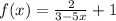
Final Answer:

(a) Yes

(b) No

(c)

`f(x)=(2)/(3-5x)+1`