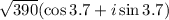Question

magnitude in exact form. Write the argument in radians and round it to twoPerform the following multiplication and write the product in trigonometric form. Write thedecimal places if necessary.(-3 + 2i)(V5 + 5i)

Answer 1

We need to write in trigonometric form the following product of complex numbers:

`\left(-3+2i\right)(√(5)+5i)`

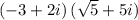
First, expanding the product, we obtain:

`\begin{gathered} \left(-3+2i\right)(√(5)+5i)= \\ \\ -3√(5)-15i+2√(5)i+10i^2= \\ \\ -3√(5)-15\imaginaryI+2√(5)\imaginaryI+10(-1)= \\ \\ -(3√(5)+10)+(-15+2√(5))i \end{gathered}`

Now, the magnitude of this number is:

`\sqrt{(-3√(5)-10)^2+(-15+2√(5))^2}=√(390)`

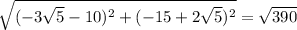
An angle with the same tangent as the argument is given by:

`\arctan\left((-15+2√(5))/(-3√(5)-10)\right)\cong0.562259`

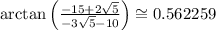
Notice that the above angle lies on the first quadrant. Nevertheless, the argument we are looking for lies in the third quadrant since both the real and the imaginary part of the complex number are negative.

Thus, we need to add π to that value to obtain the argument of this number. We obtain:

`0.562259+\pi\cong3.70`

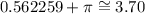
Therefore, the answer is:

`√(390)(\cos3.7+i\sin3.7)`