Question

Two cars start moving from the same point. One travels south at 20 miles per hourand the other travels west at 40 miles per hour. At what rate is the distance betweenthe cars increasing two hours later?

Answer 1

Let x, y represent the distance travelled by the cars after time, t.

We can construct a triangle for the movement of the two(2) cars, as shown below;

Let S be the distance between the two(2) cars.

By applying the Pythagoras theorem here, we have:

`\begin{gathered} S^2=x^2+y^2 \\ \text{The rate is time dependent.} \\ \text{Thus, to find the rate here, we will differentiate with respect to t;} \\ 2s\text{ }(ds)/(dt)=2x(dx)/(dt)+2y(dy)/(dt)\text{ ----eqn i)} \end{gathered}`
`\begin{gathered} (dx)/(\differentialDt t)=40\text{mph} \\ (d)/(\differentialDt t)y=20\text{mph} \\ \text{The distance x and y, after 2 hours will be;} \\ \text{Distance, x=sp}eed* time=40*2=80miles \\ \text{Distance, y=sp}eed* time=20*2=40miles \end{gathered}`

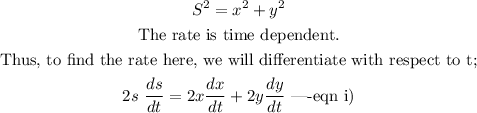
Thus, we have:

`\begin{gathered} S^2=\sqrt[]{40^2+20^2} \\ S^2=\sqrt[]{1600+400} \\ S^2=\sqrt[]{2000} \\ S=44.72 \end{gathered}`

For the rate of distance, we have:

`\begin{gathered} \text{from eqn i)} \\ 2(44.72)\text{ }(ds)/(\differentialDt t)=2(80)(40)+2(40)(20) \\ 89.44\text{ }(ds)/(\differentialDt t)=6400+1600 \\ 89.44\text{ }(ds)/(\differentialDt t)=8000 \\ (ds)/(\differentialDt t)=(8000)/(89.44) \\ (ds)/(\differentialDt t)=89.44\text{miles per hour} \end{gathered}`

Hence, the distance between the two(2) cars is changing at the rate of 89.44 miles per hour.