Question

Area = 896ft. width = L - 4

Answer 1

Let us call L the length of the hall and w its width.

Then the area of the hall is

`L* w`

and we are told that is equal to 896 ft; therefore,

`L* w=896`

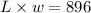
Now at this point, we have to remember that we are told that the width is 4 less than length; therefore, w = L -4 and the above equation becomes

`L*(L-4)=896`

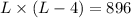
Now we have to solve for L.

Expanding the left- hand side of the above equation gives

`L^2-4L=896`

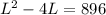
subtract 896 from both sides to get

`L^2-4L-896=0`

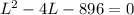
Now the quadratic formula says that if we have an equation of the form

`ax^2+bx+c=0`

then

`L=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Now in our case we have L instead of L and b = -4, c = -896; therefore,

`L=\frac{-(-4)\pm\sqrt[]{(-4)^2-4(1)(-896)}}{2(1)}`

Simplifying the right - hand side of the above equation gives

`L=\frac{4\pm\sqrt[]{16+3584}}{2}`
`x=(4)/(2)\pm\frac{\sqrt[]{16+3584}}{2}`

which gives

`L=2\pm30`

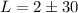
Therefore the two values of L we get are

`L=2+30=32`
`L=2-30=-28`

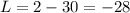
SInce lengths cannot be negative, the value L = 32 is the right answer.

Hence, the length of the hall is 32 ft.