Question

Write each fraction in terms of the LCD.5x²135xyny5x2뾿3БхуNeed Help?Watch ItAdditional MaterialseBook

Answer 1

`(4xy)/(5x^2y),(3x)/(5x^2y)`

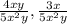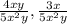
1) Since the LCD is the Least Common Multiple of those denominators we can write out:

Note that these denominators share the 5, x, and y let's prime factorize it below:

`\begin{gathered} 5xy,5x^2 \\ LCD=5x^2y \\ \end{gathered}`

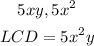
We can find it as above, prime factorizing the number and the variables.

2) So we can rewrite those fractions in terms of the LCD, dividing the LCD by each original denominator and multiplying the result by the original numerator we have:

`\begin{gathered} \\ (5x^2y)/(5xy)=x\cdot\text{ 4y}\Rightarrow(4xy)/(5x^2y) \\ \\ (5x^2y)/(5xy)=x\cdot3\Rightarrow(3x)/(5x^2y) \end{gathered}`

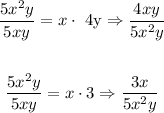
3) Hence, the answer (writing those two rations in terms of the LCD) is:

`(4xy)/(5x^2y),(3x)/(5x^2y)`