Question

An air craft factory manufactures airplane engines. The unit cost C (the cost in dollars to make each airplane engine) depends on the number of engines made. If x engines are made, then the unit cost is given by the function C (x)=0.1x^2-34x+14,266. How many engines must be made to minimize the unit cost?

Answer 1

In order to minimize the unit cost, we need to find the vertex coordinates of this function, since this will be the minimum point.

To do so, we can use the following formula for the vertex x-coordinate:

`x_v=(-b)/(2a)`

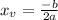
Where a and b are coefficients of the quadratic equation in the standard form:

`\begin{gathered} f(x)=ax^2+bx+c \\ C(x)=0.1x^2-34x+14266 \\ a=0.1,b=-34,c=14266 \end{gathered}`

So we have:

`x_v=(-b)/(2a)=(-(-34))/(2\cdot0.1)=(34)/(0.2)=170`

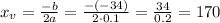
So the number of engines that should be made to minimize the unit cost is 170 engines.