Given information:
Mass of ball = 0.500 kg
Speed of ball = 5.90 m/s
Force = 9.50 N
Radius of the circular path = ?
Solution:
The force acting on the ball is given by
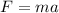
Where m is the mass and a is the circular acceleration of the ball.
The circular acceleration of the ball is given by
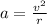
Substituting (a) into the above equation, we get
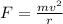
Re-writing the equation for radius (r), we get
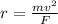
Finally, substitute the given values and solve for radius (r)
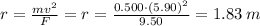
Therefore, the radius of the circular path of the ball is 1.83 meters.