Question

A tank in the shape of a hemisphere has a diameter of 16 feet. If the liquid that fills the tank has a density of 93 pounds per cubic foot, what is the total weight of the liquid in the tank, to the nearest full pound?

Answer 1

We can do the following steps to solve the exercise:

Step 1: We find the volume of the tank. For this, we use the formula to calculate the volume of a hemisphere.

`\begin{gathered} V=(2)/(3)\cdot\pi\cdot r^3 \\ \text{ Where} \\ V\text{ is the volume} \\ r\text{ is the radius of the sphere} \end{gathered}`

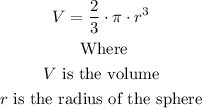
Then, we have:

`r=\frac{\text{diameter}}{2}=(16ft)/(2)=8ft`
`\begin{gathered} V=(2)/(3)\cdot\pi\cdot r^3 \\ V=(2)/(3)\cdot\pi\cdot(8ft)^3 \\ V=(2)/(3)\cdot\pi\cdot8^3ft^3 \\ V=(2)/(3)\cdot\pi\cdot512ft^3 \\ V\approx1072.33ft^3\Rightarrow\text{ The symbol }\approx\text{ is read 'approixmately'} \end{gathered}`

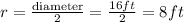
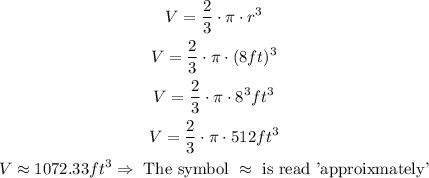
Step 2: We apply the density formula to find the total weight of the liquid in the tank.

`\text{Density }=\frac{\text{ Mass}}{\text{Volume}}`

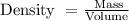
We replace the know values into the above formula.

`\begin{gathered} \text{Density }=\frac{\text{ Mass}}{\text{Volume}} \\ 93(lb)/(ft^3)=\frac{\text{ Mass}}{1072.33ft^3} \\ \text{ Multiply by }1072.33ft^3\text{ from both sides} \\ 93(lb)/(ft^3)\cdot1072.33ft^3=\frac{\text{ Mass}}{1072.33ft^3}\cdot1072.33ft^3 \\ 93lb\cdot1072.33=\text{ Mass} \\ 93lb\cdot1072.33=\text{ Mass} \\ 99,727lb\approx\text{ Mass} \end{gathered}`

Therefore, the total weight of the liquid in the tank rounded to the nearest full pound is 99,727 pounds.