Question

is y= 5/2x - 3 and 5x = 2y - 4 parallel or perpendicular or neither?is y=5/2x-3 and 5x = 2y - 4 parallel or perpendicular or niether

Answer 1

Recall that two lines are parallel if their slopes are equal and two lines are perpendicular if the product of their slopes is -1.

Now, notice that the first equation is given in slope-intercept form

`y=mx+b,`

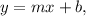
where m is the slope. Therefore, the slope of the first line is 5/2.

To be able to compare the slopes we have to determine the slope of the second line. To determine the slope of the second line, we will take the given equation to the slope-intercept form.

To put the second equation in slope-intercept form, first, we divide the equation by 2:

`(5x)/(2)=y-2.`

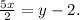
Then, we add 2:

`\begin{gathered} y-2+2=(5)/(2)x+2, \\ y=(5)/(2)x+2. \end{gathered}`

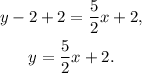
Therefore, the slope of the second line is 5/2.

Since both lines have the same slope, we can conclude that they are parallel.

Answer: The lines with equations

`\begin{gathered} y=(5)/(2)x-3, \\ 5x=2y-4 \end{gathered}`

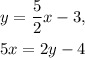
are parallel.