Question

Plot five points on the parabolic,the vertex, two points to the left of the vertex, and two points to the right of the vertex

Answer 1

Step-by-step explanation

Step 1

find the vertex,

when you have a equation in the standard form

`y=ax^2+bx+c`

the vertex is given by

`x=-(b)/(2a)`

hence,

`\begin{gathered} y=ax^2+bx+c\Rightarrow y=-2x^2 \\ so \\ a=-2 \\ b=0 \\ so,\text{ x= -}(0)/(2(-2))=0 \\ so,\text{ the vertex is x= 0 ( or y- A}\Xi s) \end{gathered}`

evaluate when x= 0 to find the coordinate of the vertex

`\begin{gathered} y=-2(0)^2=0 \\ so,\text{ vertex=(0,0)} \end{gathered}`

P1(0,0)

Step 2

now, 2 poins to the left

a)

for x=-1

`\begin{gathered} y=-2x^2 \\ y=-2(-1)^2=-2(1)=-2 \\ \text{hence} \\ P2(-1,-2) \end{gathered}`

P2(-1,-2)

b)when x=-2

`\begin{gathered} y=-2x^2 \\ y=-2(-2)^2=-2(4)=-8 \\ \text{hence} \\ P3(-2,-8) \end{gathered}`

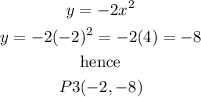
Step 3

2 points to the rigth

a)

for x=1

`\begin{gathered} y=-2x^2 \\ y=-2(1)^2=-2(1)=-2 \\ \text{hence} \\ P4(1,-2) \end{gathered}`

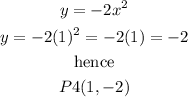
P4(1,-2)

b)when x=2

`\begin{gathered} y=-2x^2 \\ y=-2(2)^2=-2(4)=-8 \\ \text{hence} \\ P3(2,-8) \end{gathered}`

Step 4

I hope this helps you