Question

Da'Janigue had to wrap two boxes. The Red Box was 3 inches by 5 inches by 2 inches. The Blue Box was 6 inches by 5 inches and 1 inch. a. What is the volume of each box? b. What is the Surface Area of each box? C. Which has more Surface Area and by how much? d. Is it true that if two boxes have the same volume they will have the same surface area? Why or why not and give an example.

Answer 1

Given data:

The dimension of the red box is 3 inches by 5 inches by 2 inches.

The dimension of the blue box is 6 inches by 5 inches and 1 inches.

a)

The volume of the red box is,

`\begin{gathered} V=(3\text{ in)(5 in)(2 in)} \\ =30in^3 \end{gathered}`

The volume of the blue box is,

`\begin{gathered} V^(\prime)=(6\text{ in)(5 in)(1 in)} \\ =30in^3 \end{gathered}`

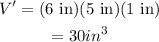
Thus, the volume of red box as well as blue box is 30 cubic-inches.

b)

The surface area of the red box is,

`\begin{gathered} SA=2(3*5+5*2+3*2) \\ =62in^2 \end{gathered}`

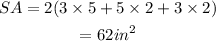
The surface area of the blue box is,

`\begin{gathered} SA=2(6*5+5*1+1*6) \\ =82in^2 \end{gathered}`

Thus, the surface area of red box is 62 sq-inches, and the surface area of the blue box is 82 sq-inches.

c)

The difference in the surface area of the blue box compare to red box is,

`\begin{gathered} \Delta=82in^2-62in^2 \\ =20in^2 \end{gathered}`

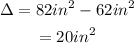
Thus, the surface area of the blue box is greater than red box, by 20 sq-inches.

d)

Thus, No it is not true that if two boxes have same volume they will have same surface area because volume represents the capacity of the body whereas surface area is the amount require to cover the body both of them are different things the above example prove that.