Question

Part A: Simplify the expression. Show all work.Part B: What is the domain of the function? Show all work.Part C: Explain why the expression in the denominator must be set equal to zero when determining the function'sdomain.

Answer 1

`\begin{gathered} (4)/(6m^2)-(5-m^2)/(4m)=(4\cdot2-(5-m^2)\cdot3m)/(12m^2)=(8-(15m-3m^3))/(12m^2)= \\ =(8-15m-3m^3)/(12m^2) \end{gathered}`

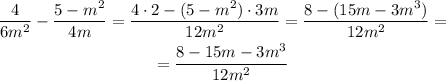
B. The domain of a function is the set that contains every possible value for the independent variable (in this case, m). Given that you cannot divide by zero then

`\begin{gathered} 12m^2\\e0 \\ m^2\\e0 \\ m\\e0 \end{gathered}`

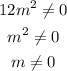
Then, the domain is all real numbers except zero.

C. The expression in the denominator must be set equal to zero because you can't divide by zero.