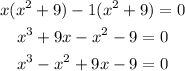Zeros of a polynomial can be defined as the points where the polynomial becomes zero as a whole.
But the zeros of the polynomial are at x=1 and x=3i.
But one of the zeros above is a complex number. So, we have;
![\begin{gathered} x=1 \\ x^2=-9 \\ x=\sqrt[]{-9} \\ x=\pm3i \\ x=3i \\ x=-3i \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ewk9cfjjotpbdvbxpmndknb7tbs4wobhtz.png)
Thus, the missing zero of the polynomial is negative 3i (-3i).
(b) Thus, the polynomial in a factored form is;
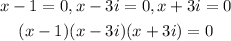
(c) In standard form, we have;
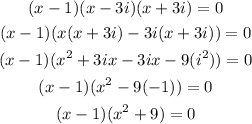
We expand further, we have;