Question

Find the unknown measures. Round lengths to the nearesthundredth and angle measures to the nearest degree.10 cm15 cmR

Answer 1

In a right triangle, we can use the pythagorean theorem to find the side lengths.

Algebraically, pythagorean theorem is:

`a^2+b^2=c^2`

Alternately, it is:

`\text{Leg}^2+\text{AnotherLeg}^2=\text{Hypotenuse}^2`

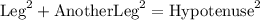
Given,

Hypotenuse = 15

Leg = 10

Let's find QP:

`\begin{gathered} 10^2+\text{AnotherLeg}^2=15^2 \\ 100+QP^2=225 \\ QP^2=225-100 \\ QP^2=125 \\ QP=\sqrt[]{125} \\ QP=\sqrt[]{25*5} \\ QP=\sqrt[]{25}*\sqrt[]{5} \\ QP=5\sqrt[]{5} \end{gathered}`

With respect to Angle R, we can write:

`\begin{gathered} \cos R=(10)/(15) \\ R=\cos ^(-1)((10)/(15)) \\ R=48.19\degree \end{gathered}`

We know 3 angles in a triangle add to 180 degrees. So, we can write:

`\begin{gathered} \angle Q+\angle P+\angle R=180 \\ \angle Q+90+48.19=180 \\ \angle Q+138.19=180 \\ \angle Q=180-138.19 \\ \angle Q=41.81\degree \end{gathered}`

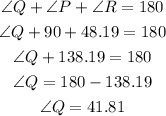
The answers are:

`\begin{gathered} QP=5\sqrt[]{5}=11.18\text{ cm} \\ \angle R=48\degree \\ \angle Q=42\degree \end{gathered}`