Question

5) without graphing determine if the points (3,6),(8,-4) and (-6,-24) do or do lie on a straight line

Answer 1

Three or more points are collinear (belong to the same line), if slope of any two pairs of points is same. We can compute the slope for the the given points. The slope formula is given by

`m=(y_2-y_1)/(x_2-x_1)`

where, in our case,

`\begin{gathered} (x_1,y_1)=(3,6) \\ (x_2,y_2)=(8,-4) \end{gathered}`

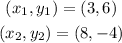
If we substitute these values into the slope formula, we have

`m=(-4-6)/(8-3)`

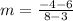
which gives

`\begin{gathered} m=(-10)/(5) \\ m=-2 \end{gathered}`

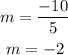
Now, we can compute the slope for the other couple of coordinates. If we take

`\begin{gathered} (x_1,y_1)=(3,6) \\ (x_2,y_2)=(-6,-24) \end{gathered}`

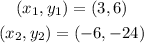
and we substitute these values into the slope formula, we have

`m=(-24-6)/(-6-3)`

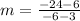
which gives

`\begin{gathered} m=(-30)/(-9) \\ m=(10)/(3) \end{gathered}`

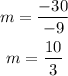
By comparing both slopes, we can see they are different. If the three points lie on a line, the slope must be the same. Then, these points do not belong to a straight line.