Question

Just the answer and as many as can be help

Answer 1

`\begin{gathered} A=w^2+4w \\ A=4w+45 \end{gathered}`

To solve the given system of equations:

1. Substitute the A by the value given in the other equation (equal the equations):

`w^2+4w=4w+45`

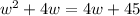
2. Leave in one side of the equation those terms with the variable w and solve it:

`\begin{gathered} w^2+4w-4w=45 \\ w^2=45 \\ w=\sqrt[]{45} \\ \\ w_1\approx6.70 \\ w_2\approx-6.70 \end{gathered}`

Then, the system of equations have two solutions.

Since w is the width of a rectangle it cannot be a negative value. Just one of the solutions is viable.

There are two solutions, but only one is viable