The given information is represented in the following diagram:
We can solve this problem by dividing this diagram into two right triangles to find the distance between each lorry and the vertical mast, and then add these distances.
The first triangle is formed with the lorry located to the East. The depression angle is 65°, then let's use tangent to find the distance from E to the mast:
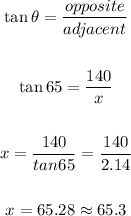
Now, the second triangle is the one formed with the lorry at the west, so:
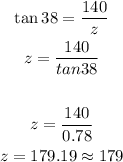
Now, the distance between the two lorries is:
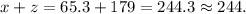
The answer is 244 (corrected to 3 s.f.)