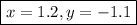Question

Solve each system of equations:
7x-4y=12.8
4x-7y=12.5

Answer 1

`x = 1.2, y = -1.1`

Explanation:

One methodology to solve a system of equations is to get the coefficients of one of the variables equal so that it can be eliminated by either addition or subtraction of the transformed equations

Looking at the two equations:

`7x-4y=12.8 \dots[1]`

`4x-7y=12.5\dots[2]`

we can make the coefficients of y the same by multiplying [1] by 7 and [2] by 4

Multiplying [1] by 7 :

`7(7x - 4y) = 7 (12.8)\\49x - 28y = 89.6\dots[3]`

Multiplying [2] by 4:

`4(4x-7y) = 4(12.5)\\\\16x - 28y = 50\dots[4]\\`

Since the y coefficients are the same, we can eliminate the y term by subtracting equation [2] from equation [1]

[1] - [2]:

`49x - 28y - (16x - 28y) = 89.6 - 50`

`49x - 16x - 28y + 28y = 39.6`

`33x = 39.6`

`x = (39.6)/(33)`

`x = 1.2`

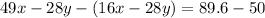
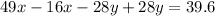
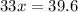
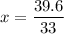
Substitute for x in Equation [1]

`7x - 4y = 12.8\\\\7(1.2) - 4y = 12.8\\\\8.4 - 4y = 12.8\\\\`

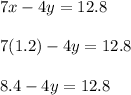
Subtract 8.4 from both sides:

`8.4 - 8.4 - 4y = 12.8 - 8.4\\\\-4y = 4.4\\\\`

Divide both sides by -4:

`(-4y)/(-4) = (4.4)/(-4)\\\\y = - 1.1`

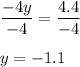
Solution:

`\boxed{x=1.2, y = -1.1}`