Question

The table shows various values of a linear function f (x).

Answer 1

Observe the table values carefully.

It is mentioned that the table represents a linear data distribution.

This means all the given points (x, f(x)) in the table will lie on the same line.

So, we take any two points from the table and form the equation of the straight line.

Consider that the equation of a line passing through two given points is given by,

`y-y_1=(y_2-y_1)/(x_2-x_1)\cdot(x-x_1)`

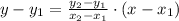
Consider the two points be (0,1) and (2,7),

`\begin{gathered} (x_1,y_1)=(0,1) \\ (x_2,y_2)=(2,7) \end{gathered}`

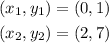
Then the equation of the line can be obtained as follows,

`\begin{gathered} y-1=(7-1)/(2-0)\cdot(x-0) \\ y-1=(6)/(2)x \\ y-1=3x \end{gathered}`

In order to find the expression of the inverse function, interchange the variables and write the equation in explicit form y=f(x).

Interchanging the variables,

`x-1=3y`

Writing in explicit form,

`\begin{gathered} 3y=x-1 \\ y=(1)/(3)(x-1) \end{gathered}`

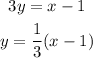
So the inverse function is,

`f^(-1)(x)=(1)/(3)(x-1)`

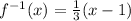
Substitute x=10 in this inverse function,

`\begin{gathered} f^(-1)(10)=(1)/(3)(10-1) \\ f^(-1)(10)=(1)/(3)(9) \\ f^(-1)(10)=3 \end{gathered}`

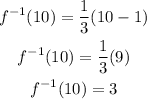
Thus, the value of the inverse function at the given point is 3.

Therefore, 1st option is the correct choice.