Question

Find the number of units of oil that are to be produced to maximize the profit if…

Answer 1

First we have to find the profit function P(x).

`\begin{gathered} P\mleft(x\mright)=R\mleft(x\mright)-C\mleft(x\mright) \\ P(x)=41x-2x^2-(x^2+17x+4) \\ P(x)=41x-2x^2-x^2-17x-4 \\ P(x)=-3x^2+24x-4 \end{gathered}`

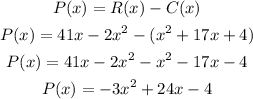
The maximum value of the quadratic function is the vertex as it opens downward. Finding the vertex, we have:

`\begin{gathered} Vx=(-b)/(2a)=(-24)/(2(-3))=(-24)/(-6)=4 \\ \text{ The x-coordinate of the vertex is x=4} \end{gathered}`

We see that the number of units needed to maximize the profit is 4 units and it satisfies the condition of being between 0 and 13 units.

The answer is x=4.