Question

How does the graph of f(x) = 3√x-5 compare to the graph of g(x) = √x?

Answer 1

Step-by-step explanation:

Given the parent function:

`f(x)=3\sqrt[]{x-5}`

If f(x) is multiplied by 1/3, we have:

`\begin{gathered} (1)/(3)f(x)=(1)/(3)*3\sqrt[]{x-5} \\ =\sqrt[]{x-5} \end{gathered}`

This means that f(x) has been shrunk vertically.

Next, we have:

`\begin{gathered} \sqrt[]{(x-5)+5}=\sqrt[]{x} \\ g(x)=\sqrt[]{x} \end{gathered}`

Thus:

`g(x)=(1)/(3)f(x+5)`

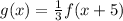
This is a vertical compression and horizontal translation left by 5 units.

Thus, the graph of f(x) is shrunk vertically and was moved to the left 5 units with re