Question

Given the following matrices A, B, and C with a scalar “k," 27 1 A = B = 3 4 3 4 Let k = 2 Commutative Property of Addition: A + B = B + A Show the Commutative Property of Addition: [:] [::] - [:$][:] Show all work using the Daum Equation Editor. Insert your image here:

Answer 1

You have the following matrices A and B:

`\begin{gathered} A=\begin{bmatrix}{1} & {2} & \\ {3} & {4} & {} \\ {} & & \end{bmatrix} \\ B=\begin{bmatrix}{1} & {1} & \\ {3} & {4} & {} \\ {} & & \end{bmatrix} \end{gathered}`

In order to verify the commutative property A + B = B + A, remind that when you add two matrices, the elements of the new matriz are the result of the sum element by element of both matrices. For example, for the case of A+B, you have:

`\begin{gathered} A+B=\begin{bmatrix}{1} & {2} & \\ {3} & {4} & {} \\ {} & & \end{bmatrix}+\begin{bmatrix}{1} & {1} & \\ {3} & {4} & {} \\ {} & & \end{bmatrix}=\begin{bmatrix}{1+1} & 2+{1} & \\ {3+3} & 4+{4} & {} \\ {} & & \end{bmatrix} \\ A+B=\begin{bmatrix}{2} & {3} & \\ {6} & {8} & {} \\ {} & & \end{bmatrix} \end{gathered}`

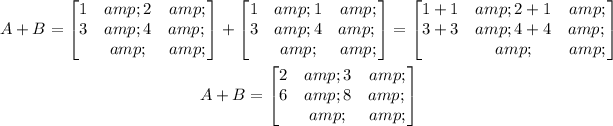
and for the case of B+A:

`\begin{gathered} B+A=\begin{bmatrix}{1} & {1} & \\ {3} & {4} & {} \\ {} & & \end{bmatrix}+\begin{bmatrix}{1} & {2} & \\ {3} & {4} & {} \\ {} & & \end{bmatrix}=\begin{bmatrix}{1}+1 & 1+{2} & \\ {3+3} & 4+{4} & {} \\ {} & & \end{bmatrix} \\ B+A=\begin{bmatrix}{2} & {3} & \\ {6} & {8} & {} \\ {} & & \end{bmatrix} \end{gathered}`

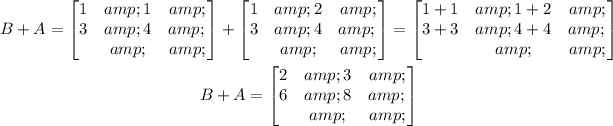
As you can notice, the result for the two cases is the same. With this the commutative property of addition is verified.