If using the method of completing the square to solve the quadratic equation x²– 8x–1=0, which number would have to be added to "complete the square"?

Question

asked Nov 14, 2023 198k views

1 Answer

Thomas McNamee · Answer 1 · 2023-11-18T12:04:53+0000

To complete squares we first need to leave the variables in one side of the equation:

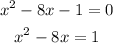
$\begin{gathered} x^2-8x-1=0 \\ x^2-8x=1 \end{gathered}$

Now we take the coefficient of the linear term, we divide it by two and squared the result. We add the result in borh sides of the equation:

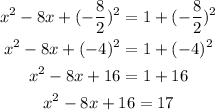
$\begin{gathered} x^2-8x+(-(8)/(2))^2=1+(-(8)/(2))^2 \\ x^2-8x+(-4)^2=1+(-4)^2 \\ x^2-8x+16=1+16 \\ x^2-8x+16=17 \end{gathered}$

the left side is now a complete squared:

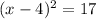
Therefore the number that we had to add in both sides of the equation is 16.