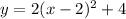Question

The vertex of the parabola below is at the point (2, 4), and the point (3, 6) is on the parabola. what is the equation of the parabola?

Answer 1

Given:

Vertex ===> (h, k) (2, 4)

The parabola passes through the point: (x, y) ==> (3, 6)

Let's find the equation of a parabola.

To find the equation, use the general equation of a parabola with vertex (h, k):

`y=a(x-h)^2+k_{}`

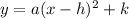
Where:

(h, k) ==> (2, 4)

(x, y) ==> (3, 6)

Substitute values into the general equation:

`\begin{gathered} 6=a(3-2)^2+4 \\ \\ 6=a(1)^2+4 \\ \\ 6=a+4 \end{gathered}`

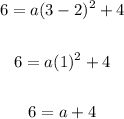
Subtract 4 from both sides:

`\begin{gathered} 6-4=a+4-4 \\ \\ 2=a \\ \\ a=2 \end{gathered}`

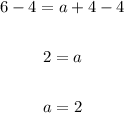
Substitute 2 for a, and input the values of the vertex (h, k) in the general vertex equation:

`y=2(x-2)^2+4`

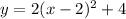
Therefore, the equation of the parabola is:

`y=2(x-2)^2+4`

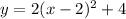
ANSWER:

`y=2(x-2)^2+4`