Question

The prompt's to solve the triangle. I've gotten the side lengths down, but I'm not too sure about the angle measures. Can anyone help?

Answer 1

Given:

`\begin{gathered} b=7 \\ c=3 \\ \angle A=41^(\circ) \end{gathered}`

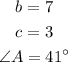
To find: The missing sides and angles

Explantion:

The formula of cosine,

`a=\sqrt[]{b^2+c^2-2bc\cos A}`

Substituting the given values we get,

`\begin{gathered} a=\sqrt[]{3^2+7^2-2(3)(7)\cos 41^(\circ)} \\ =\sqrt[]{9+49-42\cos41^(\circ)} \\ =\sqrt[]{26.3021} \\ =5.12857 \\ \approx5.1 \end{gathered}`

Thus, the missing side length is a = 5.1.

Using the sine formula,

`\begin{gathered} (\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c) \\ (\sin41^(\circ))/(5.1)=(\sin B)/(3)=(\sin C)/(7) \end{gathered}`

Solving first two terms we get,

`\begin{gathered} (\sin41^(\circ))/(5.1)=(\sin B)/(3) \\ \sin B=(3\sin41^(\circ))/(5.1) \\ =\sin ^(-1)\mleft(0.39\mright) \\ =22.70 \\ B\approx23^0 \end{gathered}`

Thus, the measure of angle B is 23 degrees.

Using the angle sum property,

`\begin{gathered} A+B+C=180^(\circ) \\ 41+23+C=180 \\ C=180-64 \\ C=116^(\circ) \end{gathered}`

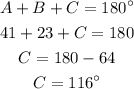
Thus, the measure of angle C is 116 degrees.

Final answer: The missing angles and sides are,

`\begin{gathered} \angle B=23^(\circ) \\ \angle C=116^(\circ) \\ BC=a=5.1 \end{gathered}`