Question

Identify the two tables which represent quadratic relationships.х01233у3456X012.3c-4-8- 10у-10Х012344у440х12.3-2.4-8у-160Х12.321400у012.3 40-22.у

Answer 1

Let the quadratic equation in the general form be,

`\begin{gathered} y=ax^2+bx+c \\ a\\e0 \end{gathered}`

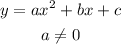
Checking option (1),

Finding the values of a,b,c by substituting the three coordinates and checking if the fourth one satisfies it or not,

`\begin{gathered} 3=a(0)^2+b(0)+c \\ c=3 \\ 4=a(1)^2+b(1)+3 \\ 1=a+b\ldots\text{.}\mathrm{}(1) \\ 5=a(2)^2+2b+3 \\ 2=4a+2b \\ 1=2a+b\ldots\ldots\text{.}(2) \end{gathered}`

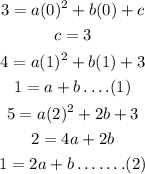
Using equaiton (1) and (2),

a=0 and b=1.

As a cannot have value 0 hence the given option is not a quadratic equation.

Checking option (2),

Finding the values of a,b,c by substituting the three coordinates and checking if the fourth one satisfies it or not,

`\begin{gathered} -4=a(0)^2+b(0)+c \\ c=-4 \\ -8=a(1)^2+b(1)-4 \\ a+b=-4\ldots\ldots\text{.}(3) \\ -10=4a+2b-4 \\ 2a+b=-3\ldots\ldots\text{.}(4) \end{gathered}`

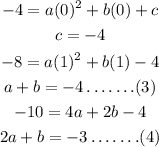
Solving equation (3) and (4),

`\begin{gathered} 2a+2b-2a-b=-8+3 \\ b=-5 \\ a=1 \end{gathered}`

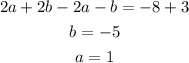
Checking the fourth coordinate,

`\begin{gathered} y=x^2-5x-4 \\ y=3^2-5(3)-4 \\ y=9-15-4 \\ y=-10 \end{gathered}`

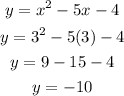
Thus, (3,-10) satifies the given quadratic.

Thus, option (2) represents a quadratic equation.

Checking option (3),

Finding the values of a,b,c by substituting the three coordinates and checking if the fourth one satisfies it or not,

`\begin{gathered} 4=a(0)^2+b(0)+c \\ c=4 \\ -4=a(1)^2+b(1)+4 \\ a+b=-8\ldots\text{.}(5) \\ -4=4a+2b+4 \\ 2a+b=-4\ldots\ldots\text{.}(6) \end{gathered}`

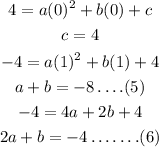
Solving equation (5) and (6),

`\begin{gathered} 2a+b-a-b=-4+8 \\ a=4 \\ b=-12 \end{gathered}`

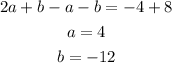
Checking the fourth coordinate,

`\begin{gathered} y=4x^2-12x+4 \\ y=4(3)^2-12(3)+4 \\ y=36-34+4 \\ y=4 \end{gathered}`

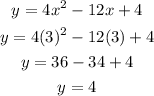
Thus, (3,4) satisfies the quadratic.

Thus, option (3) represents the quadratic.

Thus, option (2) and (3) are the two of the options which represents the quadratic.