Given the function
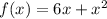
And the point (-2, -8). Therefore:
line passing through Q(–3, f(x))
We have that x = -3, so
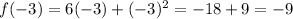
Then, the slope of line between (-2,-8) and (-3,-9) is:
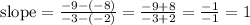
Answer: slope = 1
line passing through Q(–2.5, f(x))
x = -2.5, therefore
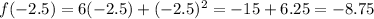
The slope of line between (-2,-8) and (-2.5, -8.75) is:
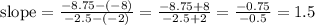
Answer: slope = 1.5
line passing through Q(–1.5, f(x))
x = -1.5, then
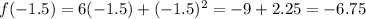
The slope of line between (-2,-8) and (-1.5, -6.75) is:
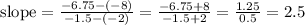
Answer: slope = 2.5
The slope of the tangent line to the graph of f at P(-2, -8)
The slope of the tangent is equal to the 1st derivative:

Then substitute x = -2
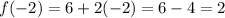
Answer: slope = 2