Question

A company sells widgets. The amount of profit, y, made by the company, is the selling price of each widget, x, by the given equation. Using this equation, find out what price the widgets should be sold for, to the nearest cent, for the company to make the maximum profit. y = -x^2+ 101x – 900

Answer 1

We want maximum profit, which is the max value of y.

We basically want for which x value, we have y as the maximum.

First,

let's take the derivative of y:

`\begin{gathered} y=-x^2+101x-900​ \\ y^(\prime)=-2x+101 \end{gathered}`

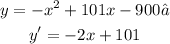
Maximum is when the derivative is equal to 0. So, the x-value when derivative is 0:

`\begin{gathered} y^(\prime)=-2x+101 \\ 0=-2x+101 \\ 2x=101 \\ x=(101)/(2) \\ x=50.5 \end{gathered}`

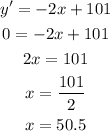
To get max profit, the widgets should be sold at $50.50