Question

Determine the zeros of the given polynomial function and the multiplicity of each zero. List the zeros from smallest to largest. If the zero is not an integer then use a fraction (not a decimal).F(x)=(3x+2)^5(x^2-10x+25)1st zero, x= Answer for part 1 with a multiplicity of Answer for part 22nd zero, x= Answer for part 3with a multiplicity of Answer for part 4

Answer 1

• 1st zero: x=-2/3 with a multiplicity of 5.

,

• 2nd zero: x=5 with a multiplicity of 2.

Explanation:

Given the function:

`F\mleft(x\mright)=\mleft(3x+2\mright)^5\mleft(x^2-10x+25\mright)`

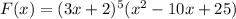
First, factorize the quadratic expression: x²-10x+25

`\begin{gathered} x^2-10x+25=x^2-5x-5x+25 \\ =x(x-5)-5(x-5) \\ =(x-5)(x-5) \end{gathered}`

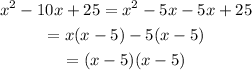
Therefore, we can rewrite F(x) as:

`F(x)=(3x+2)^5(x-5)^2`

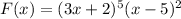
Solving for the zeroes:

`\begin{gathered} (3x+2)^5=0 \\ \text{Subtract 2 from both sides} \\ 3x=-2 \\ \text{Divide both sides by 3} \\ x=-(2)/(3)\text{ (5 times)} \end{gathered}`

• 1st zero: x=-2/3 with a multiplicity of 5.

`\begin{gathered} (x-5)^2=0 \\ x=5\text{ (twice)} \end{gathered}`

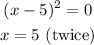
• 2nd zero: x=5 with a multiplicity of 2.