Question

11 The function f (t) = -5t² + 20t+60 models the approximate height of an object seconds after it is launched. How many seconds does it take the object to hit the ground? (Enter onlythe number)(a)(b) Graph the function from part A.POINTLINEEDIT LABELUNDOREDORESETDELETEPARABOLAA10090-8070-.605040302010

Answer 1

We are given the function f(t) = -5t^2 + 20t + 60.

To find the time it will take for the object to hit the ground, we need to remember that the height of an object on the ground is zero. So, f(t) must be equal to zero. We will solve for the t value or values that will make this statement true.

`\begin{gathered} f(t)=-5t^2+20t+60 \\ 0=-5t^2+20t+60 \\ 0=-5(t^2-4t-12) \\ 0=t^2-4t-12 \\ 0=(t-6)(t+2) \\ t=6,-2 \end{gathered}`

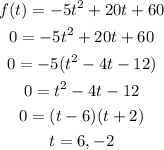
We find that t = 6 or t = -2 will make the function equal to zero. But because t represents time, it cannot have a negative value.

Therefore, the answer is that it will take 6 seconds before the object hits the ground.

To graph the function, we can solve for its vertex using:

`V(-(b)/(2a),f(x))`

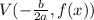
The x-coordinate of the parabola is:

`\begin{gathered} x=-(20)/(2(-5)) \\ \\ x=2 \end{gathered}`

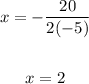
The y-coordinate is:

`\begin{gathered} f(2)=-5(2^2)+20(2)+60 \\ f(2)=-20+40+60 \\ f(2)=80 \end{gathered}`

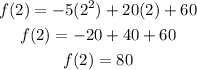
We can now use this vertex, (2, 80) and the x-intercepts (-2, 0) and (6, 0) to sketch the graph.